Hubraum, Brennraum, Verdichtung: Berechnung

Das Thema „Verdichtung” ist eine Angabe, die viele einfach so hinnehmen. Gerade bei Zweitaktmotoren wie den 250ern von Victoria ist diese Information jedoch eigentlich unzureichend, zumal sich die rechnerische und effektive Verdichtung erheblich unterscheiden.

Nun ist es nicht weiter schwer, derlei zu berechnen, beispielsweise, welches Brennraumvolumen ihr braucht, um eine bestimmte Verdichtung zu erzielen. Allerdings gilt es dabei ein paar Feinheiten zu beachten.

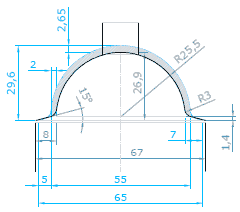
Die Basis der Berechnungen ist Verdichtung a = (Hubraum b + Brenn­raumvolumen c) ÷ Brennraumvolumen c. Die Beispiele gehen von 67 mm Bohrung aus.

Abschnitte dieser Seite:

• Berechneter und effektiver Hubraum
• Brennraum und Brennraumvolumen
• Berechnung: das effektive Brennraumvolumen
• Brennraumvolumen für gewünschte Verdichtung berechnen
• Die optimale Brennraumform

Berechneter und effektiver Hubraum

Für die folgenden Berechnungen benötigen wir zunächst einmal die Fläche der Bohrung. Die Formel zur Berechnung ist Fläche A = r² × Pi (hier genügt 3,1416). Das macht bei 67 mm 35,2 cm².

Der Hubraum ist diese Fläche × dem Hub, ein Zylinder. Bei 70 mm Hub sind das 247 cm³. Der Brennraum hat damit erst einmal nichts zu tun.

Bei Zweitaktmotoren ist das nur die halbe Wahrheit, wenn auch korrekt. Wenn es nämlich zur Verdichtung geht, ist die Höhe ab dem Schließen der Ausströmkanäle wichtig - das ist eine Annäherung zur Berechnung des effektiven Hubraums. Das stimmt wiederum nicht ganz, weil dieses Schließen nach und nach vor sich geht und die Vorfüllung im Kurbelwellenraum noch eine Rolle spielt. Lassen wir das beiseite, bleiben noch 50 mm Hub und 176 cm³ Hubraum. Das entspricht zum Beispiel etwa einer Verdichtung von 1:5,6 statt 1:7,2.

Brennraum und Brennraumvolumen

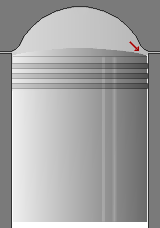
[ ± ]. Die Quetschfalte.

Das Volumen eines Brennraums ist - speziell bei asymmetrischen Quetschfalten - nicht einfach zu berechnen. Besser ist es, ihn mit einer Einweg­spritze (zum Beispiel 10 ml) auszulitern, zumin­dest den Teil im Zylinderkopf (denn auch hier stimmt das noch nicht ganz). Das ergibt (beim normalen Kopf der Victoria KR 26) 45,5 cm³.

Das ist jedoch noch nicht das ganze Brennraumvolumen - denn a) schließt je nach Stärke der Fuß– und Kopfdichtungen der Kolben bei OT mindestens einen Millimeter unter der Oberkante des Zylinders ab (+ Stärke der Kopfdichtung). Andererseits (b) hat der Kolben eine Erhöhung von 5 mm. Da derlei ebenfalls sehr schwierig zu berechnen ist, solltet ihr wieder auslitern. Es hilft, das Wasser mit einem Tropfen Spülmittel zu entspan­nen, das jedoch zügig durch die Kolbenringe abfließen kann - egal (Symbol: lachen) .

Andererseits klappt es auch, das effektive Brennraumvolumen bei bekannter, rechnerischer Verdichtung genau zu berechnen - siehe nächster Abschnitt.

Berechnung: das effektive Brennraumvolumen

Kehren wir zunächst zu der Grundformel „Verdichtung a = (Hubraum b + Brennraumvolumen c) ÷ Brennraumvolumen c” zurück (a = (b + c) ÷ c). Die muss jetzt nach Brennraumvolumen (c) aufgelöst werden. Der Hubraum ist dabei der berechnete.

Wir haben in der Formel eine Definitionslücke, c, und dafür wird {0} eingesetzt. Dann werden die Seiten der Gleichung vertauscht: (b + c) ÷ c = a. Wird das auf beiden Seiten mit dem Bruchnenner (c) multipliziert, ergibt sich b + c = a × c. Nachdem (a × c) negativ auf die andere Seite gebracht ist, haben wir b + c - a × c = 0 (oder 0 = b + c - a × c).

Gleich geschafft (Symbol: zwinkern) ! b wird negativ auf die andere Seite gebracht (c - a × c = -b) und c ausgeklammert ((-a + 1) × c = -b). Daraus ergibt sich, beidseitig durch (-a + 1) geteilt, c = -(b ÷ (-a + 1)). Klartext: Brennraumvolumen c = -(Hubraum b ÷ (-Verdichtung a + 1)). Äh, zweimal Minus, wie war das nochmal? Das hebt sich hier auf, also Brennraumvolumen c = Hubraum b ÷ (Verdichtung a - 1). Bei einer Verdichtung von 1:6,2 (normale KR 26) ergibt sich 247 cm³ ÷ 5,2 = 47,8 cm³ (statt der 45,5 ausgeliterten cm³ im Kopf).

Die Differenz (2,3 cm³) können wir ruhig als Konstante in weitere Berechnungen einsetzen. Würde hier nur das im Kopf ausgeliterte Volumen benutzt, wäre die Verdichtung höher.

Brennraumvolumen für gewünschte Verdichtung berechnen

Mit dem geballten Wissen von oben (Symbol: lachen) ist das nun ein Klacks. Nehmen wir an, ihr wollt die Verdichtung der KR 26 N (moderat!) von 1:7,2 auf 1:7,5 erhöhen.

Hubraum b ÷ (Verdichtung a - 1) = Brennraumvolumen c, also 247 ÷ (7,5 - 1) = 38,0 cm³. Zieht ihr noch die Konstante von oben ab, landet ihr bei 35,7 cm³ für den Kopf selbst. Irgendwo in der Mitte liegt die Wahrheit (Symbol: zwinkern) .

Die optimale Brennraumform

Erstens ist eine seitlich angebrachte Kerze wie hier zwar praktisch, weil leichter herauszuschrauben, jedoch unglücklich bei der Entzündung und dem Flammbild im Kopf. Die Kerze gehört in die Mitte des Brennraums, wenn das geht (was bei Viertaktern mit zwei Ventilen je Zylinder nicht immer klappt, weil es die Ventilgröße einschränkt).

Zweitens sind seitliche Quetschfalten wie beim N–Kopf sehr ungewöhnlich. Der Hintergedanke war wohl dabei, die entzündeten Gase leicht Richtung Auslass zu beschleunigen. Optimal für die gleichmäßige Verbrennung und geringere thermische Belastungen ist jedoch eine rundum laufende, breitere Quetschfalte mit einem Kugelsegment in der Mitte.

Ein Umbau ist durch aufschweißen möglich, da muss jedoch ein Profi dran. Genug Fleisch für das Kerzengewinde in der Mitte ist gegeben. 10,5 bis 12,7 mm braucht es, vorhanden sind 14,2. Wer so etwas vorhat, sollte als Basis den niedrig verdichteten Kopf der KR 26 nehmen. Der ist günstiger, weil das originale Kerzenloch noch seitlicher von der Brenn­raummitte liegt und die Schweißgrenze nicht an die seitlichen Quetsch­falten des neueren Typs reicht. Ausdrehen und planen ist auf einer Planscheibe kein Problem - so ein Kugelausdreher vorhanden ist.